Innledning
For noen dager siden kom en venn av meg over en rekke intervju spørsmål hvor en rekke kandidater ble stilt et sett med relativt enkle og greie oppgaver. Disse oppgavene var ment for å teste grunnleggende forståelse av programmering. Basert på kommentarene i dokumentet kommer det tydelig frem at mange av kandidatene slet med oppgavene, og av den grunn valgte jeg å løse disse for gøy. Jeg valgte å gjøre det i Python da dette er mitt minst brukte programmeringspråk. Det var i utgangspunktet ikke satt noe krav til meg selv på tid eller noe, men ettersom jeg gjorde det rundt 04:00 på natten, ble det en liten utfordring i seg selv, samt at jeg ønsket å se hvor raskt jeg kunne løse de ulike oppgavene.
Link til alle oppgaver med kommentarer finner du her.
Ca tid brukt på oppgavene: 15 minutter.
Oppgave 1
Finn alle oddetall mellom 1 og 100. Jeg valgte å legge til for både oddetall og partall, da dette var en enkel løsning. Det er en simpel funksjon som sjekker om det vil bli noen tall i reserve etter å ha delt på 2. Dersom det er 0 har vi et partall, hvis ikke har vi et oddetall. Så kjører vi en for loop fra 1 til 100, og sjekker om tallet er oddetall eller partall.
#Odd and even numbers
def odd_even(n):
if n % 2 == 0:
return "even"
return "odd"
for i in range(1, 101):
print(str(i) + " is " + odd_even(i))
#Output
#1 is odd
#2 is even
#3 is odd
#...
Oppgave 2
Summer alle tall i fra tall X til tall Y, eksempelvis 1 til 100. Jeg valgte å bruke en enkel for loop for å summere tallene.
Vi erklærer en variabel ans som 0, og legger til hvert tall for hver iterasjon i loopn.
#Sum numbers in range
def sum_numbers(start, end):
ans = 0
for i in range(start, end+1):
ans += i
return ans
print(sum_numbers(1,5))
#Output
#15
Oppgave 3
Tell ned fra 700 til 200 ved å hoppe 13 tall. Jeg valgte å bruke en while loop for å telle ned, og trekke fra 13 for hvert iterasjon. Vi sender inn tallene for start (700), slutt (200) og antall vi trekker fra for hver iterasjon. For hver gang vi teller ned printer vi ut det nye tallet.
#Count down in increments
def countdown(start, end, increment):
while(start >= end):
print(start)
start -= increment
countdown(700, 200, 13)
#Output
#687
#674
#661
#...
Oppgave 4
Lag en ny kortstokk, og trekk ut et tilfeldig kort. For denne oppgaven valgte jeg å opprette 4 ulike typer kort, på engelsk Diamonds (D), Hearts (H), Clubs (C) og Spades (S). Etter dette kjørte jeg gjennom en for loop med 13 iterasjoner (det er 13 kort per type i en kortstokk), og la til en fra hver type for hvert tall. Deretter har vi en metode å trekke kort. For å trekke kort finner vi først et tilfeldig tall ved hjelp av random.randint(), for så å hente ut kortet, og så sletter vi kortet fra bunken. I dette tilfellet forsvinner 5D.
#Create card deck
types = ['H', 'D', 'S', 'C']
cards = []
def create_deck():
for i in range(13):
for type in types:
cards.append(str(i+1) + type)
#Pull random card
def pull():
x = random.randint(0, len(cards) - 1)
card = cards[x]
cards.remove(card)
return card
create_deck()
print(cards)
print(pull())
print(cards)
#Output
#['1H', '1D', '1S', '1C', '2H', '2D', '2S', '2C', '3H', '3D', '3S',
'3C', '4H', '4D', '4S', '4C', '5H', '5D', '5S', '5C', '6H', '6D',
'6S', '6C', '7H', '7D', '7S', '7C', '8H', '8D', '8S', '8C', '9H',
'9D', '9S', '9C', '10H', '10D', '10S', '10C', '11H', '11D', '11S',
'11C', '12H', '12D', '12S', '12C', '13H', '13D', '13S', '13C']
#5D
#['1H', '1D', '1S', '1C', '2H', '2D', '2S', '2C', '3H', '3D', '3S',
'3C', '4H', '4D', '4S', '4C', '5H', '5S', '5C', '6H', '6D', '6S',
'6C', '7H', '7D', '7S', '7C', '8H', '8D', '8S', '8C', '9H', '9D',
'9S', '9C', '10H', '10D', '10S', '10C', '11H', '11D', '11S', '11C',
'12H', '12D', '12S', '12C', '13H', '13D', '13S', '13C']
Oppgave 5
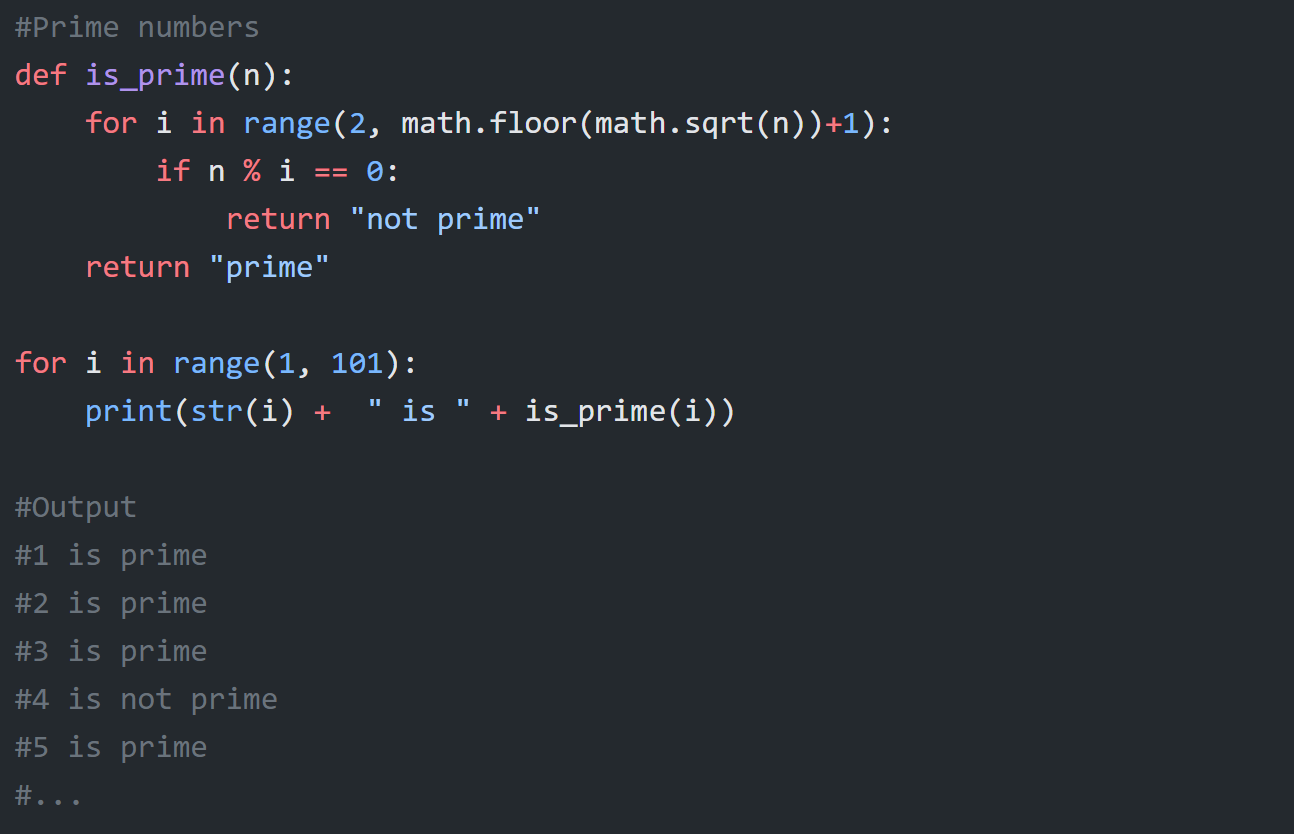
Finne alle primtall mellom X og Y, enkelt og greit finne om et tall er primtall. For å finne om et tall er primtall må man sjekke om det kan deles på noen av tallene fra 2 til tallet minus 1 sier en gjerne. Teknisk sett trenger man kun å ta opp til halvparten av tallet for å finne ut om det er et primtall. Dette er fordi dersom det er et tall som kan deles på et tall større enn halvparten, vil det også kunne deles på et tall mindre enn halvparten. En kan også senke tallet enda mer og ta kvadratroten av tallet, da dette er den høyeste verdien som kan være en faktor for tallet.
#Prime numbers
def is_prime(n):
for i in range(2, math.floor(math.sqrt(n))+1):
if n % i == 0:
return "not prime"
return "prime"
for i in range(1, 101):
print(str(i) + " is " + is_prime(i))
#Output
#1 is prime
#2 is prime
#3 is prime
#4 is not prime
#5 is prime
#...